Теоретически и практически доказано, что тепловые воздействия на постоянный магнит могут приводить как к обратимым, так и необратимым изменениям намагниченности, а, следовательно, и индукции магнитного поля в рабочей области. Следует обратить внимание на то, что в этом разделе не рассматриваются необратимые тепловые изменения параметров магнитотвёрдого материала как такового, то есть структурные изменения. Необратимые и обратимые явления, рассматриваемые в данном разделе, хоть и возникают в материале постоянного магнита, но связаны как с характеристиками этого материала, так и с характером магнитной нагрузки на магнитотвёрдый материал, то есть с соотношением размеров магнита и конфигурацией магнитной системы – с положением линии нагрузки.

Обратимые изменения магнитных свойств стабилизированного магнитотвёрдого материала можно оценивать соответствующими коэффициентами, например температурным коэффициентом магнитной индукции, который определяется по формуле:

,

где: В₂₀ – индукция при 20°С,

В_Т – индукция при температуре Т °С,

Т - температура в °С.

Подобным образом принято оценивать изменения и других параметров, например, таких как  коэрцитивная сила, магнитная энергия.

У магнитов из магнитотвёрдого материала температурный коэффициент магнитной индукции зависит, кроме химического состава и структуры материала ещё и от относительных размеров магнита (размагничивающего фактора), степени предварительного размагничивания, а так же и от температуры.

В таблице 1 приведены значения температурного коэффициента магнитной индукции в точке максимума магнитной энергии для сплавов типа альнико.

Таблица 1

Экспериментальные значения температурного коэффициента индукции α_в(%/°С) в области максимума магнитной энергии в зависимости от температуры

Отметим, что значения температурных коэффициентов  в таблице 1 приведены в области максимума магнитной энергии, так как считается, что магнитные системы из магнитотвёрдых материалов системы альни и альнико следует конструировать так, чтобы рабочая точка магнитов находилась именно в этой области – условие оптимального использования магнитного материала.

Как было отмечено выше, магнитные системы из магнитотвёрдых материалов системы альни и альнико желательно конструировать так, чтобы рабочая точка магнитов находилась  области максимума магнитной энергии, однако по разным причинам это удаётся не всегда. Следовательно, температурного коэффициента индукции α_В обратимых изменений магнитной индукции надо знать и для произвольной рабочей точки. Приближённую оценку температурного коэффициента α_В обратимых изменений магнитной индукции для любой рабочей точки магнитов из сплавов типа альнико можно получить, если известны температурные зависимости остаточной индукции (∆B_rθ/B_r20) и коэрцитивной силы (∆H_сθ/H_С20) материала [1].

1) если ∆B_rθ/B_r20  < 0,  ∆Н_сθ/Н_с20  < 0, то

,

2) если ∆B_rθ/B_r20  > 0,  ∆Н_сθ/Н_с20  < 0, то

,

3) если ∆B_rθ/B_r20  < 0,  ∆Н_сθ/Н_с20  > 0, то

,

где - тангенс угла наклона касательной в рабочей точке к оси Н (при определении k надо учитывать масштабы по осям  В и Н),

µ_а = -В/Н – абсолютная магнитная проницаемость в рабочей точке,

µ_r,rev – проницаемость возврата (абсолютная).

Экспериментальные данные о температурных изменениях остаточной индукции В_r и коэрцитивной силы Н_сВ приведены в таблице 2.

Таблица 2

Относительные изменения (%) остаточной индукции и коэрцитивной силы в интервале температур минус 180 …плюс 600 °С

Покажем на нескольких примерах, как проводить расчёты температурного коэффициента по приведённым выше выражениям.

Пример 1. Пусть для магнита, изготовленного из материала марки ЮНДК35Т5, требуется определить температурный коэффициент индукции при температуре 200⁰С в точке, соответствующей (ВН)_max.

По таблице 2 находим значения ∆B_rθ/B_r20 = -3% и  ∆Н_сθ/Н_с20  = - 2.5 % , что соответствует случаю ∆B_rθ/B_r20 < 0, ∆Н_сθ/Н_с20 < 0. По кривой размагничивания материала (рис. 1) определяем μ_а  = 6.25 и μ_r,rev  = 2.

Для температурного коэффициента получаем следующее значение:

,

что, как видно, находится в хорошем согласии с данными таблицы 1 (-0.015%/⁰C).

Пример 2. Пусть для того же магнита требуется определить температурный коэффициент при температуре – 80 ⁰С.

По таблице 2 находим значения ∆B_rθ/B_r20  =  2 % и  ∆Н_сθ/Н_с20  =  -1.5 % , что соответствует случаю ∆B_rθ/B_r20  > 0, ∆Н_сθ/Н_с20  < 0. Как и в примере № 1 μ_а  =  6.25 и  μ_r,rev  = 2. Для температурного коэффициента получаем следующее значение

.

В таблице 1 экспериментальное значение температурного коэффициента составляет 0,025 %/⁰C.

Пример 3. Пусть для магнита, изготовленного из материала ЮНДК24 (рис.2), требуется определить температурный коэффициент при температуре  100  ⁰С.

По таблице 2 находим значения ∆B_rθ/B_r20  = - 2% и  ∆Н_сθ/Н_с20  = 3% , что соответствует случаю ∆B_rθ/B_r20  < 0,   ∆Н_сθ/Н_с20   > 0. В этом случае -  μ_а  = 37,  μ_r,rev  = 1, k  =  5. Для температурного коэффициента получаем следующее значение –

.

В таблице 1 даны фактические экспериментальные значения температурного коэффициента, которое составляет минус 0,015 %/⁰C.

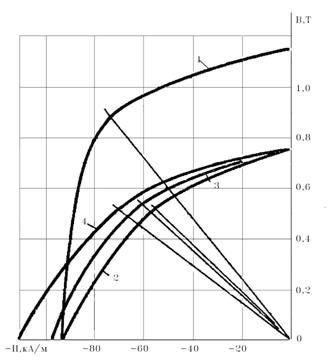
Рис. 1. Кривые размагничивания:

1 - ЮНДК31Т3БА; 2- ЮНДК34Т5; 3- ЮНДК35Т5Б; 4- ЮНДК35Т5

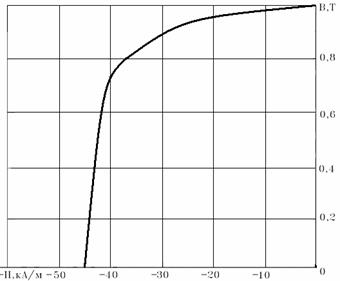
Рис. 2. Кривая размагничивания материала ЮНДК24

Рассмотрим некоторые особенности характеристики стабильности ферритовых магнитотвёрдых материалов.

Как было отмечено выше, ферритовые постоянные магниты обладают структурной стабильностью неограниченное время. Однако у ферритовых магнитов достаточно велики обратимые изменения магнитных параметров. Температурный коэффициент остаточной индукции ферритовых магнитотвёрдых материалов составляет  минус (0,18 … 0,2)%/°С. Существенна также зависимость коэрцитивной силы по намагниченности от температуры, приведённая на рис. 3. Для оценки тепловых изменений коэрцитивной силы по намагниченности можно ввести аналогично тому, как это сделано для остаточной намагниченности, температурный коэффициент коэрцитивной силы:

.

Для ферритовых магнитотвёрдых материалов температурный коэффициент коэрцитивной силы по намагниченности в интервале температур от  минус 60°С до 250°С можно оценивать величиной βНсм≈  0,3 %/°С.

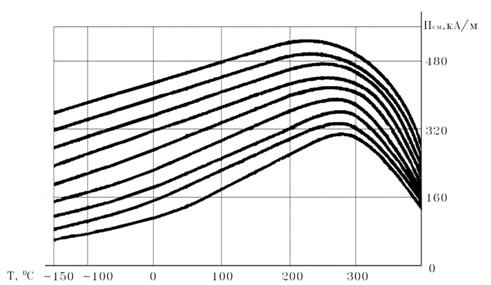
Рис. 3. Зависимость коэрцитивной силы по намагниченности ферритов бария и стронция от температуры

Так как магнитные параметры ферритовых магнитотвёрдых материалов зависят  от температуры, то при вариациях температуры в пределах обратимых изменений этих параметров также обратимо будут изменяться и значения магнитных полей постоянного магнита. Принимая независимость нагрузки на постоянный магнит (размагничивающий фактор) от температуры, можно получить следующее выражение для температурного коэффициента магнитного поля, как отдельного постоянного магнита, так и магнитного поля магнитной системы:

или, если учесть, что, как правило, χ_ТN <<1,

,

где: χ – реверсивная восприимчивость магнитотвёрдого материала,

N – размагничивающий фактор.

Из приведённого выражения следует, что величина обратимых изменений магнитного поля магнитной системы определяется не только величиной обратимых изменений магнитных параметров магнитотвёрдого материала (температурным коэффициентом остаточной намагниченности материала и температурными изменениями реверсивной восприимчивости), но и типом магнитной системы и соотношением размеров её элементов. В зависимости от знака изменения реверсивной восприимчивости при изменениях температуры температурный коэффициент магнитного поля магнитной системы может быть как больше, так и меньше температурного коэффициента изменения остаточной намагниченности.

Для ферритовых магнитотвёрдых материалов температурный коэффициент изменения остаточной намагниченности всегда отрицательный, а температурный коэффициент коэрцитивной силы по намагниченности в интервале температур от отрицательных до примерно 250°С положительный, следовательно, при нагревании в этом диапазоне температур намагниченность уменьшается, а коэрцитивная сила увеличивается, значит < 0. Действительно, обработка экспериментальных данных по температурным зависимостям кривых размагничивания различных ферритовых магнитотвёрдых материалов дает следующий результат:  .

Таким образом, для ферритовых магнитотвёрдых материалов (ферриты бария и стронция)  температурный коэффициент обратимых изменений индукции магнитного поля магнитной системы может быть определён следующим выражением:

.

Температурный коэффициент остаточной намагниченности РЗМ-Со магнитотвёрдых материалов лежит в пределах минус (0,04…0,06)%/° С,  а температурный коэффициент коэрцитивной силы по намагниченности составляет минус (0,25 … 0,3)%/° С.

Температурный коэффициент остаточной намагниченности Nd-Fe-B магнитотвёрдых материалов имеет значение минус 0,0 7%/⁰С в интервале температур минус 40 ⁰С … 20°С  и минус 0,12 %/ ⁰С в интервале температур (10 … 100)^°С.

Температурный коэффициент коэрцитивной силы по намагниченности равен минус 0,07%/°С в интервале температур (- 40 … 20) °С и минус 0,8 %/°С в интервале температур (10 … 100)°С.

Так же, как и для ферритовых магнитотвёрдых материалов, величина обратимых изменений магнитного поля магнитной системы будет определяться не только величиной обратимых изменений магнитных параметров магнитотвёрдого материала (температурным коэффициентом остаточной намагниченности материала и температурными изменениями реверсивной восприимчивости), но и типом магнитной системы и соотношением размеров её элементов. Для редкоземельных магнитотвёрдых материалов температурные коэффициенты изменения остаточной намагниченности и коэрцитивной силы всегда отрицательные, следовательно, при нагревании и намагниченность и коэрцитивная сила будут уменьшаться, результатом этого является > 0. Действительно, обработка экспериментальных данных по температурным зависимостям кривых размагничивания различных редкоземельных материалов дала для РЗМ-Со материалов   и для  Nd-Fe-B материалов: .

Таким образом, для РЗМ-Со магнитотвёрдых материалов температурный коэффициент обратимых изменений индукции магнитного поля магнитной системы может быть определён следующим выражением:

,

а для Nd-Fe-B магнитотвёрдых материалов –

.

В таблице 3 приведены сводные данные по обратимой температурной нестабильности для всех групп магнитотвёрдых материалов.

Таблица 3

Температурные коэффициенты обратимых изменений характеристик магнитотвёрдых материалов и магнитного поля магнитных систем

Приведём несколько примеров расчёта обратимых температурных изменений магнитного поля магнитных систем на постоянных магнитах.

Пример 1. Определить величину обратимых изменений индукции магнитного поля в магнитной системе с ферритовыми постоянными магнитами. Температура изменяется от 20⁰С  до 100⁰С, размагничивающий фактор магнитов в магнитной системе равен N = 0.7, внешние магнитные поля отсутствуют.

Используя данные таблицы 3, получаем:

.

Следовательно, при температуре 100°С  величина индукции магнитного поля уменьшиться на 12% , действительно:

.

Пример 2. Определить величину обратимых изменений индукции магнитного поля в магнитной системе с Nd-Fe-B постоянными магнитами. Температура изменяется от 20⁰С  до минус 60 ⁰С, размагничивающий фактор магнитов в магнитной системе равен N = 0.7, внешние магнитные поля отсутствуют.

Используя данные таблицы 3, получаем:

.

Следовательно, при температуре минус 60°С  величина индукции магнитного поля увеличится на  12%, действительно:

.

Как видно из приведённых примеров, при отличии температурных коэффициентов остаточной намагниченности магнитотвёрдых материалов почти в два раза, температурные коэффициенты индукции магнитного поля в магнитной системе оказываются одинаковыми, следовательно, сама величина температурного коэффициента обратимых изменений остаточной намагниченности ещё не позволяет делать выводы о температурных изменениях магнитного поля в магнитной системе.

Кроме того, следует обратить внимание на то, что нами не случайно выбрано в первом примере изменение температуры в сторону нагревания, а во втором примере в сторону охлаждения. Это связано с тем, что для ферритовых магнитотвёрдых материалов характерно возрастание коэрцитивной силы при нагревании в рассматриваемом диапазоне температур – положительный температурный коэффициент коэрцитивной силы (см. таблицу 3) и, следовательно, не возможно возникновение необратимых изменений намагниченности, связанных с положением рабочей точки на кривой размагничивания.

Аналогичная ситуация возникает и в случае с редкоземельными магнитотвёрдыми материалами. Но здесь коэрцитивная сила возрастает при охлаждении – отрицательный температурный коэффициент коэрцитивной силы (см. таблицу 3). То есть при использовании редкоземельных магнитотвёрдых материалов необратимые изменения величины магнитного поля в магнитной системе, связанные с положением линии нагрузки, не будут возникать при охлаждении.

Необратимые изменения магнитных свойств. Замечено, что под воздействием некоторых внешних  факторов, при эксплуатации и хранении,  ферритовые изделия подвергаются необратимым изменениям.

Под необратимыми изменениями понимается частичное размагничивание магнита под воздействием нагревания, охлаждения или воздействия внешних магнитных полей. При возвращении магнита в исходное состояние его намагниченность изменяется в соответствие с кривой возврата и не приходит в исходную точку. Восстановление первоначального состояния возможно путём повторного намагничивания. Необратимые изменения возникают в результате обратимых тепловых деформаций петли гистерезиса в том случае, если линия нагрузки магнита в магнитной системе оказывается при этих деформациях ниже колена кривой размагничивания.

У всех магнитотвёрдых материалов  при тепловых воздействиях происходит деформация петли гистерезиса.

Примеры деформации кривых размагничивания, характерные для литых, ферритовых и редкоземельных магнитотвёрдых материалов, возникающие при тепловых воздействиях, приведены на рис.3..6 и описаны в таблице 4.

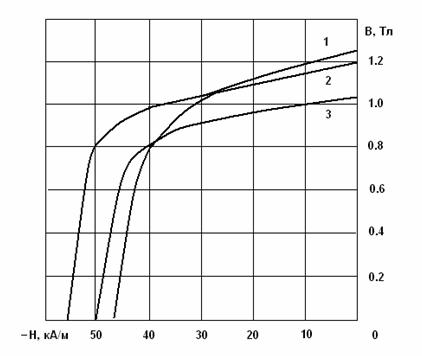
Рис. 4. Кривые размагничивания сплава ЮН14ДК24 при разной температуре.

1 – минус 180⁰С; 2 – 20⁰С; 3 – 550⁰С

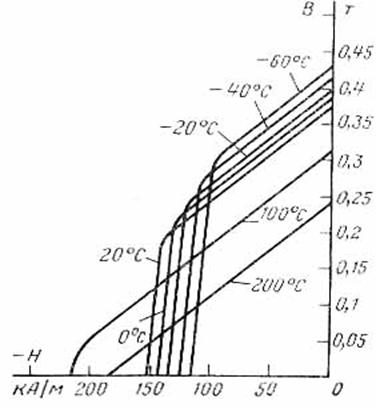
Рис. 5. Тепловые деформации кривой размагничивания ферритового магнитотвёрдого материала

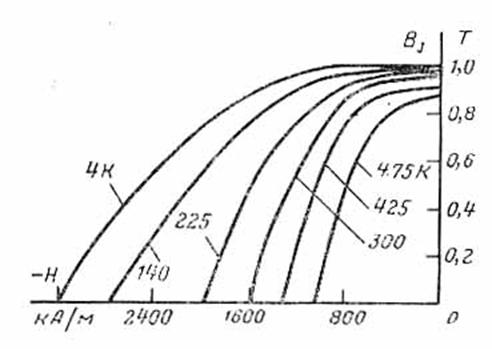
Рис. 6. Тепловые деформации кривой размагничивания редкоземельного магнитотвёрдого материала

Таблица 4

Температурные коэффициенты обратимых изменений характеристик магнитотвёрдых материалов и магнитного поля магнитных систем

На рис. 7 в качестве примера приведены кривые размагничивания магнитотвёрдого материала с B_r = 3900Гс, Н_сВ = 3200э, Н_сМ = 3300э, (ВН)_max = 3,49МГс*э (В_r = 390мТл, Н_сВ = 255кА/м, Н_сМ = 260кА/м, (ВН)_max = 27.8кДж/м³) для температур 20⁰С, -40⁰С.

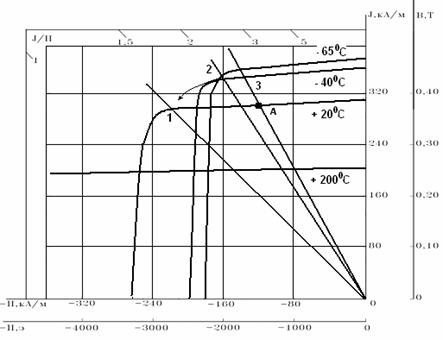
Рис. 7. Тепловые деформации кривой размагничивания ферритового магнитотвёрдого материала

На рис. 7 построена максимально возможная для данного материала при температуре 20 ⁰С нагрузочная характеристика – линия 1, которая называется  линией нагрузки и описывается  размагничивающим фактором N =H/J, равным в данном случае  N = 0,75.

Как видно из    рис. 7, при охлаждении магнитной системы с таким постоянным магнитом нагрузочная характеристика пересекает кривую размагничивания ниже колена, то есть в процессе морожения магнит будет размагничиваться собственными внутренними полями и при возвращении к исходной температуре намагниченность магнита окажется ниже, чем в исходном состоянии - частично размагниченный магнит.

При нагревании вплоть до температур, при которых коэрцитивная сила возрастает (см. рис. 3) саморазмагничивание ферритового магнита не наблюдается.

Таким образом, для ферритовых постоянных магнитов предельная положительная рабочая температура составляет примерно 300 °С.

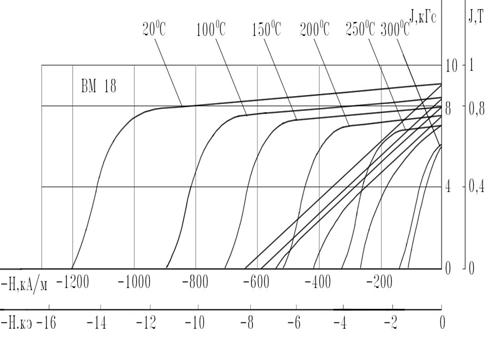
Рис. 8. Кривые размагничивания Sm-Co материала в зависимости от температуры

Предельная рабочая температура при охлаждении ферритового постоянного магнита или нагревании редкоземельного постоянного магнита и предельный размагничивающий фактор (предельно допустимая нагрузка на магнит) должны определяться в каждом конкретном случае. Покажем на примерах, как это следует делать.

Пример 1. Пусть для магнитной системы с ферритовым постоянным магнитом, изготовленным из магнитотвёрдого материала с параметрами,  приведёнными на рис. 7, требуется определить предельно допустимую нагрузочную характеристику (N - фактор), при которой не будут возникать необратимые потери индукции магнитного поля).   Температура охлаждения составляет  минус 40°С.

Проведём линию нагрузки так, как это показано на рис. 7 (линия нагрузки 2).  Это и есть искомая нагрузочная характеристика – при возвращении в начальное состояние (нагревание) точка (2), описывающее магнитное состояние магнита при температуре минус 40⁰С, переместится в точку (1), описывающую магнитное состояние магнита при температуре 20°С, что и гарантирует отсутствие необратимых изменений величины магнитного поля.

Значение размагничивающего фактора в точке (2) определяется отношением напряжённости к намагниченности и будет равно

.

Вывод:– для того чтобы магнитная система, изготовленная из рассматриваемого магнитотвёрдого материала, была устойчива при морожении до температуры минус 40°С, значение размагничивающего фактора не должно превышать 0,46.

Пример 2. Пусть для магнитной системы с ферритовым постоянным магнитом, изготовленным из магнитотвёрдого материала с характеристиками, приведёнными на рис. 7 и с нагрузочной характеристикой N = 0.4 (линия 3), требуется определить предельно допустимую температуру охлаждения, при которой не будут возникать необратимые изменения индукции магнитного поля. Эта задача решается методом последовательного приближения. Определяем значение поля Н, соответствующее точке пересечения нагрузочной характеристики магнита в магнитной системе с кривой размагничивания при комнатной температуре - точка (А) (Н_А = 120 кА/м).

По зависимостям для коэрцитивной силы по намагниченности (рис. 3) определяем для данного материала температуру, при которой достигается полученное значение поля - эта температура составляет минус 150°С. Очевидно, что при такой температуре магнит будет иметь необратимые изменения намагниченности. Возьмём среднее значение температуры, а именно: Т=(20 - 150)/2 = - 65 ⁰С.

Проводим перестроение исходной кривой размагничивания, полученной для комнатной температуры, в кривую размагничивания для температуры  минус 65°С.

Определение точки В_r (- 65°С).

.

Определение точки Н_сМ (- 65 ⁰С).

По спектру зависимостей, представленных на рис. 3, находим искомое значение Н_сМ ( - 65 °С) = 180 кА/м.

В первом приближении, что, как показывает практика, вполне достаточно для поставленной задачи, последующие построения проводятся следующим образом.

а). Проводим линию из точки Вr = 456 мТ параллельно линии наклона верхнего участка кривой размагничивания при комнатной температуре.

б). Проводим линию из точки Н_сМ = 180 кА/м параллельно нисходящему участку  кривой размагничивания при комнатной температуре.

в). Замыкаем эти две линии дугой, подобноq дуге, замыкающей кривую размагничивания при комнатной температуре.

Из описанной выше схемы и приведённых на рис. 7 построений видно, как должно быть продолжено решение задачи для определения предельной температуры. Если считать, что линия нагрузки располагается достаточно близко к колену кривой размагничивания, то тогда предельной рабочей температурой будет  минус 65°С.

Следовательно, постоянный магнит, изготовленный из магнитотвёрдого материала с указанными характеристиками в рассматриваемой магнитной системе (N = 0.4) может работать в интервале температур + 300 … минус 65°С.

Как видно из  рис. 6,8 и как следует из таблицы 4, при охлаждении магнитов из редкоземельных материалов происходит возрастание, как остаточной намагниченности, так и коэрцитивной силы, следовательно, при морожении необратимые изменения магнитного поля возникнуть не могут. При нагревании коэрцитивная сила редкоземельных магнитотвёрдых материалов уменьшается, что может привести к необратимому размагничиванию магнитов.

Расчёты, проведённые для максимально возможного  размагничивающего фактора N=1, дали следующие значения предельных рабочих температур для магнитов из редкоземельных материалов – магниты из РЗМ-Со  – +250 ⁰С … 300 ⁰С,  Nd-Fe-B –  + 150 ⁰C.

В таблице 5 представлены данные по предельным рабочим температурам для магнитов из различных магнитотвёрдых материалов.

Таблица 5

Предельные рабочие температуры для постоянных магнитов

Литература

1. Постоянные магниты: Справочник. Под ред. Ю.М. Пятина. М.: Энергия. 1971. 486 с.

К предыдущему сообщению

К следующему сообщению